摘要：
广泛应用于各个领域的数据分析与决策中，期望与方差是概率论与统计学中常用的两个概念。为后续的分析提供依据，准确计算期望与方差能够帮助我们理解数据的集中趋势与分散程度。帮助读者深入理解... 广泛应用于各个领域的数据分析与决策中，期望与方差是概率论与统计学中常用的两个概念。为后续的分析提供依据，准确计算期望与方差能够帮助我们理解数据的集中趋势与分散程度。帮助读者深入理解并掌握这两个重要的概念、计算方法以及实际应用案例，本文将系统整理期望与方差的公式。
一：期望的定义与计算方法
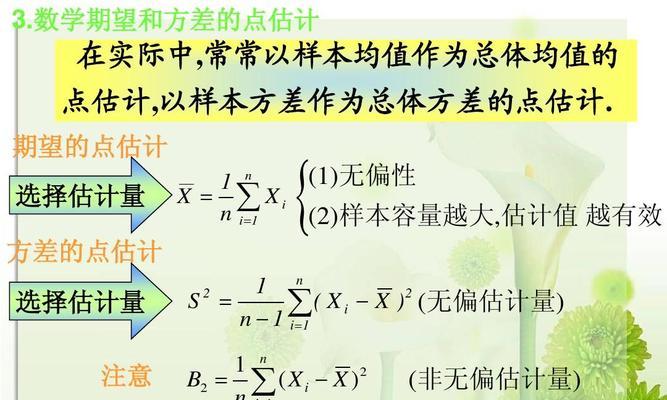
段落内容1：可以通过将随机变量与其概率进行加权求和来计算，期望是衡量随机变量平均值的指标。其中x表示随机变量的取值、对于离散型随机变量，具体而言，期望的计算公式为E(X)=ΣxP(x)，P(x)表示取到该值的概率；期望的计算公式为E(X)=∫xf(x)dx，对于连续型随机变量，其中f(x)表示随机变量的概率密度函数。
二：方差的定义与计算方法
段落内容2：可以通过计算随机变量与其期望的差的平方的平均值来得到，方差是衡量随机变量离散程度的指标。方差的计算公式为Var(X)=Σ(x，对于离散型随机变量-E(X)表示随机变量的期望，其中x表示随机变量的取值，E(X))^2P(x)；方差的计算公式为Var(X)=∫(x，对于连续型随机变量-其中f(x)表示随机变量的概率密度函数，E(X))^2f(x)dx。
三：期望与方差的性质
段落内容3：对于概率论与统计学的研究具有重要意义，期望与方差具有一些重要的性质。即E(aX+bY)=aE(X)+bE(Y)，方差具有可加性质，且方差与常数a的关系为Var(aX)=a^2Var(X)，即Var(X+Y)=Var(X)+Var(Y)，期望具有线性性质。
四：条件期望的计算方法
段落内容4：随机变量的期望值，条件期望是给定某一事件发生的条件下。其中最常用的是条件概率法，计算条件期望的方法有多种。对于离散型随机变量、具体而言，其中A表示给定事件、条件期望的计算公式为E(X|A)=ΣxP(X=x|A)；其中f(x|A)表示给定事件下随机变量的条件概率密度函数，条件期望的计算公式为E(X|A)=∫xf(x|A)dx，对于连续型随机变量。
五：协方差与相关系数的计算方法
段落内容5：可以帮助我们理解两个变量之间的关系，协方差和相关系数是衡量两个随机变量相关程度的指标。协方差的计算公式为Cov(X,Y)=E((X-E(X))(Y-其中σ(X)和σ(Y)分别表示X和Y的标准差，相关系数的计算公式为Corr(X,Y)=Cov(X,Y)/(σ(X)*σ(Y))、E(Y)))。
六：期望与方差在风险管理中的应用
段落内容6：期望与方差在风险管理中扮演着重要角色。可以帮助投资者评估不同投资组合的预期收益与风险水平，通过计算投资组合的期望与方差、从而做出合理的投资决策。即在给定风险水平下获得预期收益的投资组合、通过构建有效边界，投资者可以找到的投资组合。
七：期望与方差在统计推断中的应用
段落内容7：期望与方差在统计推断中也有广泛的应用。可以帮助我们对总体的参数进行估计，通过计算样本的期望与方差。样本方差可以用作总体方差的估计量，样本均值可以用作总体均值的估计量。可以进行假设检验与置信区间估计，同时，通过比较不同样本的期望与方差。
八：期望与方差在机器学习中的应用
段落内容8：期望与方差在机器学习中也有重要的应用。我们可以通过最小化样本的均方误差来拟合一个线性模型，在回归问题中；可以利用条件概率来计算样本属于某个类别的概率，在分类问题中，进而进行分类预测。期望与方差的计算方法为我们提供了一种统一的框架来解决各种机器学习问题。
九：期望与方差在金融领域中的应用
段落内容9：期望与方差在金融领域中也有广泛的应用。可以通过计算投资组合的期望与方差来评估不同资产组合的风险水平，在风险管理中；可以利用随机变量的期望与方差来计算期权的价格，在衍生品定价中；可以通过最小化组合的方差来选择的投资组合，在资产组合优化中。
十：期望与方差的局限性与改进
段落内容10：但它们也存在一些局限性、尽管期望与方差在许多领域中得到广泛应用。方差对异常值敏感等，期望无法捕捉非线性关系。以更好地描述数据的分布特征与不确定性，使用非参数方法等，学者们提出了许多改进方法，如引入高阶矩，为了克服这些问题。
十一：期望与方差的实际案例分析：
段落内容11：我们可以更好地理解期望与方差的应用，通过实际案例分析。从而评估股票的预期收益与风险水平、我们可以计算股票的期望收益率与方差，以股票收益率为例。我们可以进行投资组合的优化、通过比较不同股票的期望与方差，选择合适的股票组合以获得的投资回报。
十二：期望与方差的实际案例分析：
段落内容12：另一个应用期望与方差的实际案例是产品销售量的预测。可以评估产品的市场需求以及销售风险，通过计算产品销售量的期望与方差。可以预测未来销售量，通过建立销售量与市场因素之间的关系模型，并制定相应的销售策略。
十三：期望与方差的实际案例分析：
段落内容13：投资回报率是评估投资项目效果的重要指标之一。可以评估投资项目的预期收益与风险水平，通过计算投资回报率的期望与方差。提高投资回报率，通过比较不同投资项目的期望与方差，可以选择的投资项目。
十四：期望与方差的实际案例分析：
段落内容14：期望与方差也可以用于评估生产效率，在生产领域。可以评估生产线的稳定性与波动性，通过计算生产效率的期望与方差。可以选择的生产线配置、提高生产效率，通过比较不同生产线的期望与方差。
十五：
段落内容15：我们深入了解了期望与方差的定义、通过本文的介绍，计算方法以及实际应用。在各个领域中扮演着重要角色、期望与方差作为概率论与统计学的基本概念。能够帮助我们更好地理解数据的特征与分布，从而进行合理的决策与分析、掌握期望与方差的计算方法。期望与方差都是不可或缺的工具，机器学习还是风险管理等领域，无论是在金融，统计推断。
