摘要：
对数函数是高中数学中的重要概念之一，它在各个领域都有广泛的应用。本文将深入探讨对数函数的定义域以及求解方法，帮助读者更好地理解和掌握这一概念。1.对数函数的基本概念... 对数函数是高中数学中的重要概念之一，它在各个领域都有广泛的应用。本文将深入探讨对数函数的定义域以及求解方法，帮助读者更好地理解和掌握这一概念。
1.对数函数的基本概念
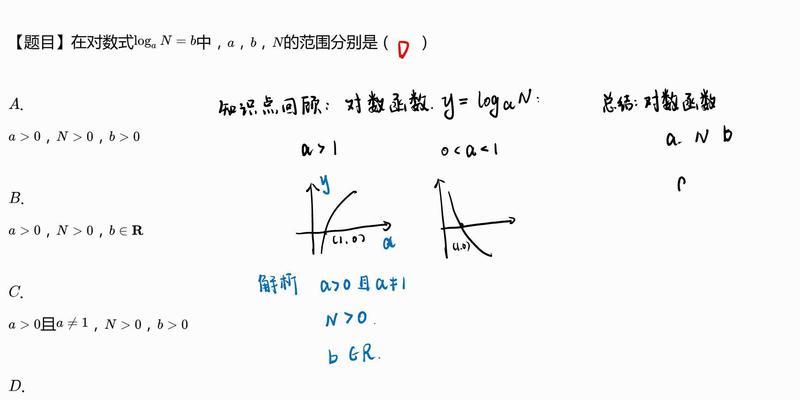
对数函数是指以某个正数为底数，将正数x映射到另一个正数y的函数。它可以表示为y=log?x，其中a为底数，x为真数，y为对数。
2.对数函数的定义域概念
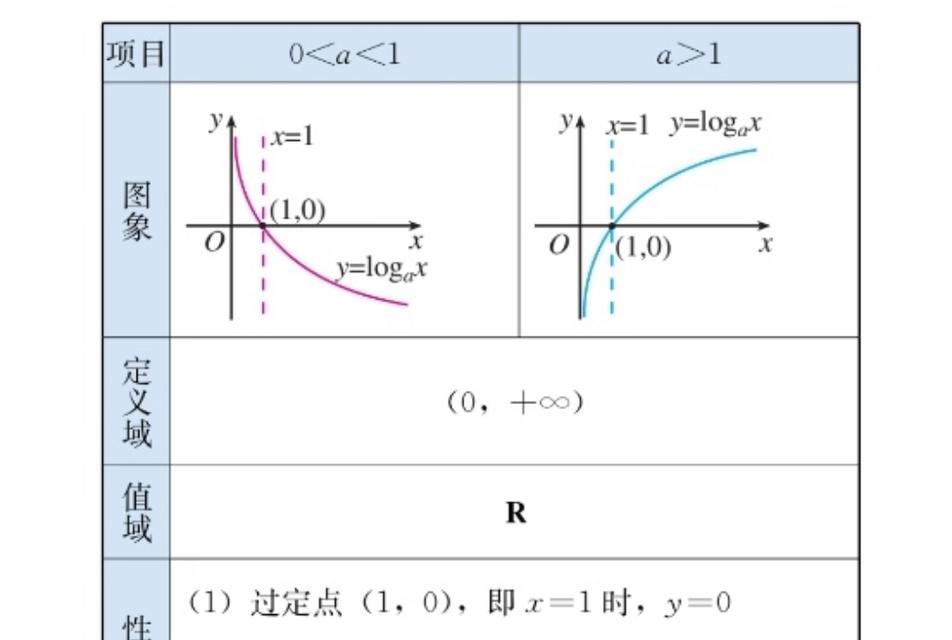
定义域是指函数中自变量（输入）的取值范围。对于对数函数来说，底数a必须大于0且不等于1，而真数x必须大于0，因此定义域为(0,+∞)。
3.以常见底数为例的定义域求解
以常见底数10为例，当对数函数y=log??x时，由于底数为10，真数x必须大于0，因此定义域为(0,+∞)。
4.特殊情况下的定义域求解
当对数函数中底数a为1时，无论真数x为何值，都会得到1作为对数函数的值。这种情况下对数函数的定义域为空集。
5.对数函数与指数函数的关系
对数函数与指数函数是互为反函数关系，它们的定义域和值域也是相互转换的。当一个函数的定义域为(0,+∞)，另一个函数的值域也为(0,+∞)。
6.复合函数中的定义域求解
当对数函数作为复合函数的一部分时，我们需要考虑整个复合函数的定义域。通过分析每个函数的定义域，并求取交集，即可得到复合函数的定义域。
7.对数函数中的负数和零的处理
对于对数函数来说，负数和零是没有意义的。在求解对数函数的定义域时，我们需要排除负数和零。
8.定义域求解与图像的关系
对数函数的定义域可以通过观察其图像来求解。当我们绘制对数函数的图像时，可以直观地看出其定义域是什么。
9.对数函数定义域相关例题分析
通过分析具体例题，我们可以更加深入地理解对数函数的定义域求解方法，掌握其求解过程。
10.对数函数定义域求解方法
了对数函数定义域求解的一般方法和步骤，帮助读者在实际问题中应用这些方法。
11.对数函数定义域的实际应用
介绍对数函数定义域在实际问题中的应用，如经济学、生物学、物理学等领域，展示对数函数的重要性。
12.对数函数定义域求解的注意事项
列举了在求解对数函数定义域时需要注意的一些常见问题和容易犯的错误，以提醒读者避免这些问题。
13.对数函数定义域求解的拓展知识
介绍了更加复杂的对数函数定义域求解方法，如对数函数组合、对数不等式等，帮助读者进一步提高对对数函数定义域的理解。
14.对数函数定义域求解思维拓展
提供一些思维拓展题，帮助读者巩固对对数函数定义域的理解，培养灵活运用知识的能力。
15.结语：对数函数定义域的重要性和应用价值
了对数函数定义域的重要性和应用价值，并鼓励读者继续深入学习对数函数及其相关知识。通过掌握对数函数的定义域求解方法，读者可以更好地应用于实际问题中，拓展数学应用的能力。
